The Enthought PDF slides give further detail on the different types of indexing that exist.¶
In [ ]:
# Import modules
import numpy as np
import matplotlib.pyplot as plt
In [ ]:
# Import modules
import numpy as np
import matplotlib.pyplot as plt
Creating 1D arrays with array() arange() and linspace()¶
In [ ]:
# Python
# Use array() to create arrays of any dimension if you already know or have the values to put
# into the array.
x = np.array([5,4,3,2,1])
# Linspace inputs are start, stop, # of elements
xls = np.linspace(0,100,100)
# arange inputs are start,stop,interval
xar = np.arange(0,100,0.9999)
#print(xar.shape)
#xls.shape
# This term tells you to pull the last value of the array out
#print( xar[-1], xls[-1])
Numpy can store numeric information (usually float() or int() data types) in 2, 3 or even N- dimensional arrays. Note that the indexing of 2D arrays goes like [row #, col #], e.g. a[3,2] gives the element at row=4 and column=3.
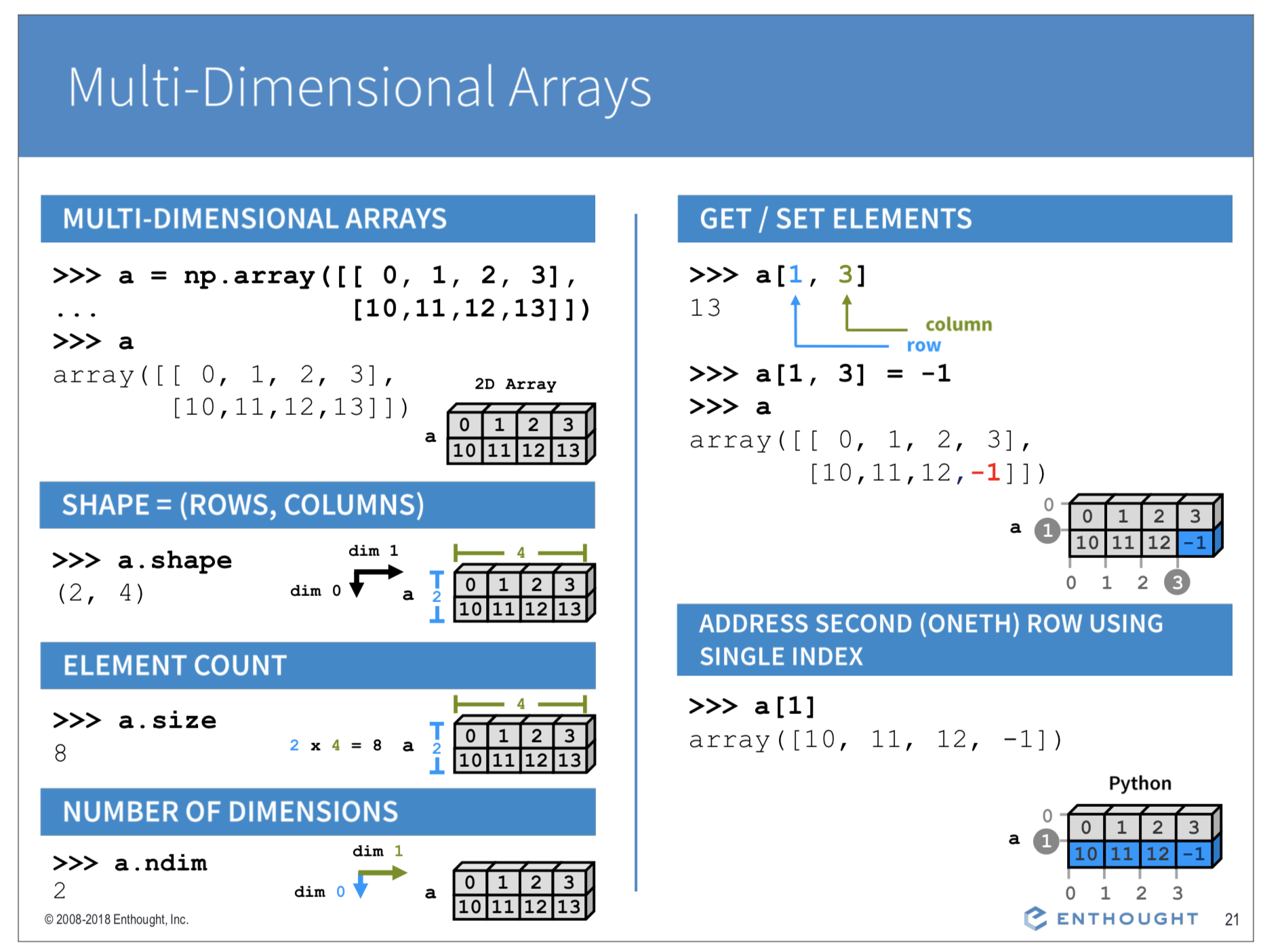
Creating 2D arrays with array(), zeros(), ones()¶
In [ ]:
# PYTHON
# Assembling a 2D array by concatenating 1D arrays.
x = np.array([[1,2,3],[3,4,5]])
print(x.shape)
# Currently this is a 1D array
y = np.array([1,2,3])
# Sometimes you need to set an array up to be 2D, so you can add data to it later.
# This should be a 2D array
y2 = np.array([1,2,3],ndmin = 2)
#print("Y has",y.ndim,"dimensions. Y2 has",y2.ndim,"dimensions")
In [ ]:
y*y2
Arithmetic on Arrays (element-wise or linear algebra)¶
By default, Numpy will try to carry out element-wise arithmetic (+,-,*,/) on arrays of like dimension. Where possible, Numpy will also use array broadcasting to make the operation work.

In [ ]:
# PYHON AND R
y + y2 #This is permitted. It takes on the higher dimensions.
y * y2 #Likewise permitted. It takes on the higher dimensions.
In [ ]:
# Examples of array manipulations.
R = np.arange(0,100,12) # Create a vector of 9 elements
# Element-wise operation. P is the same size as R.
P = R*R
# Impliclit element-wise operation.
Q = P.copy() - 3
Q = P*R
# Make R into a 3 x 3 matrix (2D array), and store it in S.
S = R.reshape(3,3)
# An array multiplication with broadcast operation.
T = S*np.array([3,2,1])
#print(T)
In [ ]:
# Object-oriented notation
#print( T.max(),np.max(T) ) #(Object-oriented notation, Functional notation)
print(T.max(axis=0),np.max(T,axis=0) ) #Take the max along the row axis
Combining arrays for data wrangling.¶
In [ ]:
#In general, when concatenating (merging or pasting together) arrays they must have the same shape and same dimensions
#help(np.concatenate)
#np.concatenate((y,y2)) # Not permitted.
#np.concatenate((y[np.newaxis,:],y2)) #Expand the dimensions of y before concatenating.
# Stack vertically. This has same effect as concatenate
# np.vstack((y,y2)) # Permitted, because arrays have the same column dimensions
# Stack horizontally.
np.hstack((y[np.newaxis,:],y2)) # Not Permitted, because y and y2 have the different row dimensions
#np.hstack((y[np.newaxis,:],y2))
Indexing and boolean operations for 2D arrays¶
In [ ]:
# Index individual row or column in 2D array
z = np.ones((100,50))
# Save a single row of z to a new variable
zr = z[9,:]
# Save a single column of z to a new variable
zc = z[:,9]
print(zc.shape,zr.shape, z.shape)
In [ ]:
# Make a 2D column vector of ones with 10 elements in it.
a = np.ones([10,1])
# Copy that column vector 10 times to make a square array.
b = np.tile(a,10)
# Make a vector of 10 elements and then place them in the diagonal of a 10 x 10 square array.
c = np.ones(10)*100
d = np.diag(c)
# Use the Matplotlib spy() function to visualize the array b+d
plt.spy(b+d,precision=10,markersize=10)
plt.show()
#print(b+d)
#np.random.randn(10)
In [ ]:
#print(d)
In [ ]:
# Check out shape, ndim, dtype
z = d+b
#print(z.shape)
#print(z.dtype)
#print(z)
In [ ]:
# Use boolean operators to change values.
z2 = z.copy()
# Find all the values equa1 to 1.
id1 = (z2 == 1)
# id1 now has a boolean record of which values are ==1.
print(id1)
In [ ]:
# Let's change all the elements equal to 1.
z2[id1] = 3.14159
#z2[z2 == 3.14159] = np.nan
print(z2)
Let's try this exercise together. How many ways can this be solved, algorithmically?

Algorithm 1:
- Create a
- Divide all elements by 3.
- Look for values with a remainder of zero.
- Create boolean array to subindex.
Algorithm 2:
- Create a
- Divide all elements in a by 3.
- Check to see which elements are equal to their integer counterparts.
Finish the notebook by solving the cells below with code.¶
In [ ]:
# Convert all the values of z2 that are > 99 into NaNs.
In [ ]:
# Make a 2D numpy array named Arr of size 10 x 10 and fill it with random values that range between 0 and 99. You can use numpy's random module
Arr = np.random.randint(100,size =100)
In [ ]:
# Use boolean indexing to replace all the values in Arr greater than 80 and less than 20 with NaNs.
In [ ]:
# Use the append() or concatenate() commands in numpy to add more columns to Arr.
Concept Review: More looping practice
In [ ]:
# We already saw that np.diag() can insert elements along the diagonal of a square array.
# Use your understanding of for loops to carry out the same operation.
# Create a 10 x 10 array of ones and then modify the center diagonal to be 101 instead of 1.
# Hint: You will need two indices, e.g i and j to specify the row and column to modify.
# Hint: You can use a boolean operator to decide which elements in the square array to modify.